あるあるミス　６年生

本日は

わり算です

今までの復習の総決算ですね

忘れてしまっている人は４・５年生のわり算をご覧下さい

復習です

必殺！「一つ下ルール！」

そして！

合言葉は！「商は上げるだけ、あまりは下げるだけ！」

算数ってやっぱり、積み上げ式の勉強なんだなぁとしみじみです

わり算につまずくと、小数のわり算も苦手に、、、とつながっていくので、その学年ごとにしっかりと定着させた方が合理的です

四捨五入、桁の理解・暗記など、これは複数の要素がありますね

「あるある」は商を四捨五入すれば良いのに、あまりをつけた不思議な答えにしてしまう子多数！

本日は

わり算です

前回の概数とは少し変わっただけなのに、注意すべき！ポイントがあるのが、「上から」の問題

けたの場合は、とにかく指示どおりで、一つ下の位ルール適用でOK！しかし、上から～けたの概数で、求めなさいという問題の場合は、答えが０．なんちゃらとなった時のみ注意が必要です

一つ下ルールは同じ、そして、上から１・２・３ケタと数えるのは同じなのですが、答えが０．□□になった時だけ注意なのです

でも、意外と普通のことなのかも

０（ゼロ）なのに、上から数える必要があるのかな？

ゼロだからこそ、上から数えない、カウントしないのです

だから、いつも一つ下を四捨五入ルールで「よし、上から（右から）数えよう！」ってところですが、いやいや、今回は０.□□だぞ？ということでゼロだから、上から数えずに、□を上から数えよう！と考えようということなのです

難しくはないのですが、忘れてしまうので、ここはチェック！

まさに、ザ！６年生！という問題でした

今までの復習すべてが詰まった問題でしたね

本日は

「くふうして」の問題です

あるあるは「なかなかみんな工夫してくれない」ということです

工夫という言葉自体が小学生にはハードル高めなのかもしれませんね

「工夫して」というよりも「こっちのが楽なんだよー」とか楽な方法で解きましょうみたいな指示の方が小学生は「楽なの？いいじゃん、やりたい！」みたいにもっと前のめりで覚えてくれるような気がします

言葉の力って大きいですよね

しかし、いたしかたない！工夫した計算は同じ数をみつけてかっこでまとめて、符号は下に下げるだけなのですが、なかなか覚えてくれず、そのままかけ算して解いてしまう子が続出してしまうので、「工夫して」という問題通り、素直に取り組みましょう

本当にそっちの方が計算ミスも減り、楽ですよ！

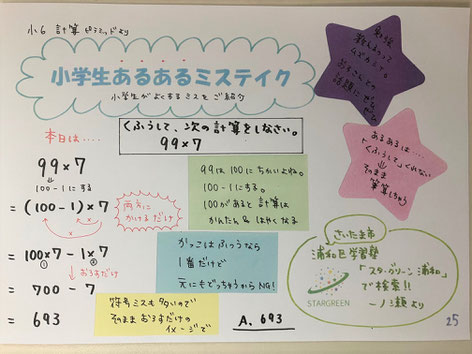
本日も

「くふうして」の計算です

前回に引き続き、「こっちの方が楽なんだよー」ですが、これまた、なかなか覚えてもらえないのです

９９は極めて、１００に近いってことは気づくはずですが、かっこの計算もミスしてしまうそもそもハードルがある子にとっては、ますます難しい気がしてしまうのです

かっこで１００－１と書くところまではOK！その後に一気にできない子が続出します

展開と言って、それぞれをかけ算すればよし、そして、符号はそのまま下ろすだけ、ですが、それぞれにかけるという発想を忘れてしまうようです

算数は一日にしてならず、毎日コツコツ解きましょう

本日も

「くふうして」です

今まではかっこの計算がからむことによって、本当はめちゃくちゃ楽になる計算がかえって小学生にとっては混乱を生んでしまうという、この「工夫して」の特徴はつかんでもらえましたかね

今回は絶対的に暗記しておいてほしいというかけ算があるので、

お知らせしておきますね

４×２５＝１００は絶対暗記です

もちろん８×２５＝２００なども覚えておくと便利なのですが、たくさん出るのが、１００になる、４×２５なのです

今までずーっとなぜか０の扱いに迷ってしまうお子さんが多いことも伝えてきたように、今までの復習として、そこも分かっている？と確認ができる問題となるのでしょう

「くふうして」というワード自体は小学校３年生から登場しますので、楽に解けるんだよと「覚えるがなぁ」と後ろ向きになってしまうお子さんを少しでも前向きに伝えてあげてくださいね

小学３年生の方でも紹介していきますね